Российско-британская школа «алгоритм» — russian-british school
Содержание:
- 1. Нет тяжёлых портфелей
- Общая характеристика
- Алгоритм за O(n3)[править]
- Минусы алгоритма Укконена[править]
- Время работы[править]
- Что дает обучение в школе “Алгоритм”
- 7. Стипендии
- Улучшения алгоритма Шуфа
- Сибирская региональная школа (колледж) Анны Муратовой
- 4. Шведский стол
- Центр Семейного Образования «Репетитор плюс школа»
- Разбираем «на пальцах»
- Электронная гимназия АНПОО «МАНО»
- Теорема Хассе
- Выводы
1. Нет тяжёлых портфелей
«Алгоритм успеха» – экспериментальная школа с мобильным электронным образованием: вместо бумажных книг дети занимаются по цифровым учебникам. Малыши пользуются электронными книгами, ученикам с 5 класса выдают планшеты, а старшеклассникам –ноутбуки. Все они подключены к цифровой образовательной платформе Lecta. Домашние задания, в том числе индивидуальные, дети получают в системе «Мобильное электронное образование» (МЭО).
Всю технику и зарядные устройства к ним выдают в школе, а после занятий дети оставляют её в классе. На уроке за гаджетами ребята проводят не больше 15–20 минут, чтобы не портить глаза.
Классическая библиотека с бумажными книгами в школе тоже есть, и дети могут ими пользоваться, при этом свыше 600 экземпляров русской классической литературы, к примеру, через кваркоды всё равно можно скачать на планшет.



Общая характеристика

Российско-британская школа «Алгоритм» – это организация, оказывающая образовательные услуги на самом высоком уровне. Здесь можно пройти обучение по российским и британским школьным программам, подготовиться к международным экзаменам и вступительным испытаниям в Oxford University. Также есть курсы по развитию личности (актерское мастерство, вокал, программирование) и сценическая лаборатория. За последние 4 года 34 выпускника школы поступили в престижные зарубежные вузы, двое – в Оксфордский университет. Среди российских высших учебных заведений слушатели курсов «Алгоритма» отдают предпочтение МГУ, ВШЭ, МГИМО.
Для учеников 9 и 11 классов общеобразовательных школ в «Алгоритме» предлагают пройти курсы ОГЭ и ЕГЭ. Учебная программа каждого слушателя формируется с учетом его цели. Это может быть глубокая подготовка к Единому государственному экзамену или же повышение знаний по отдельным предметам для улучшения школьных оценок. За каждым старшеклассником закрепляется куратор, который помогает решать все проблемные вопросы, отслеживает прогресс и держит постоянную связь с родителями подопечного.
В школе «Алгоритм» есть собственный учебный интернет-портал, где находится полный набор информации, которая требуется для самостоятельной работы. Это всевозможные тесты и интерактивные задания, цифровые ресурсы, аудио- и видеоматериалы. После заключения договора все слушатели получают к нему доступ, чтобы пользоваться в процессе обучения. Также для удобства клиентов разработан онлайн-планер, при помощи которого учащиеся уточняют расписание, отслеживают оценки и домашние задания, получают комментарии от преподавателей. Обратиться за более детальными консультациями можно, указав в специальной форме на сайте организации свое имя и номер телефона.
Формы занятий
Занятия могут проходить в очном формате в аудитории или в онлайн-режиме с использованием дистанционных компьютерных технологий. Уроки проводятся дважды в неделю и длятся по 90 минут каждый.

В ходе уроке преподаватели проверяют домашнее задание, разбирают все ошибки и сложные места, затем дают теоретический материал, после чего слушатели приступают к выполнению практических упражнений, разработанных на основе тестов предыдущих лет
Опытные учителя быстро выявляют недостатки и пробелы в знаниях своих подопечных и акцентируют внимание на их устранении
Для мониторинга прогресса слушателей используются периодические контрольные тестирования. Для того чтобы ученики были готовы к итоговому испытанию, на протяжении курса трижды организовывается пробный ЕГЭ. Он проводится в формате, максимально приближенном к реальному Единому государственному экзамену. Такой подход позволяет школьникам психологически подготовиться к стрессовой ситуации, научиться владеть собой, чтобы не терять драгоценного времени и не совершать простых ошибок.
Сроки
Занятия по подготовке к ЕГЭ рассчитаны на 8 месяцев и длятся с октября по май включительно. Группы могут стартовать в разное время в зависимости от их комплектации.
Преподаватели
Педагогический коллектив школы «Алгоритм» состоит из опытных преподавателей, среди которых эксперты ЕГЭ, члены экзаменационных и апелляционных комиссий, проверяющие работы, авторы методических и учебных пособий, победители профессиональных конкурсов. На протяжении многих лет они специализируются на подготовке школьников к Единому государственному экзамену и добиваются с ними высоких результатов. Учителя отслеживают все новшествах в сдаче ЕГЭ, тщательно изучают их и адаптируют свои учебные программы в соответствии с изменениями.
Алгоритм за O(n3)[править]
Рассмотрим сначала наивный метод, который строит дерево за время , где — длина исходной строки . В дальнейшем данный алгоритм будет оптимизирован таким образом, что будет достигнута линейная скорость работы.
| Определение: |
| Неявное суффиксное дерево (англ. implicit suffix tree, IST) строки — это суффиксное дерево, построенное для строки без добавления . |
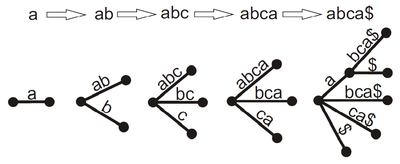
Пример построения суффиксного дерева алгоритмом Укконена.
Алгоритм последовательно строит неявные суффиксные деревья для всех префиксов исходного текста . На -ой фазе неявное суффиксное дерево для префикса достраивается до для префикса . Достраивание происходит следующим образом: для каждого суффикса подстроки необходимо спуститься от корня дерева до конца этого суффикса и дописать символ .
Алгоритм состоит из фаз. На каждой фазе происходит продление всех суффиксов текущего префикса строки, что требует времени. Следовательно, общая асимптотика алгоритма составляет .
Псевдокод алгоритма за O(n3)править
for i = 1 .. n
for j = 1 .. i
treeExtend(s)
Замечание: на первый взгляд, более логичным подходом кажется добавление всех суффиксов строки в дерево по очереди, получив сразу алгоритм со временем работы . Однако осуществить улучшение данного алгоритма до линейного времени работы будет намного сложней, хотя именно в этом и заключается суть алгоритма МакКрейта.
Минусы алгоритма Укконена[править]
Несмотря на то, что данный алгоритм является одним из самых простых в понимании алгоритмов для построения суффиксных деревьев и использует online подход, у него есть серьёзные недостатки, из-за которых его нечасто используют на практике:
- Размер суффиксного дерева сильно превосходит входные данные, поэтому при очень больших входных данных алгоритм Укконена сталкивается с проблемой memory bottleneck problem(другое её название thrashing).
- Для несложных задач, таких как поиск подстроки, проще и эффективней использовать другие алгоритмы (например поиск подстроки с помощью префикс-функции).
- При внимательном просмотре видно, что на самом деле алгоритм работает за время , используя столько же памяти, так как для ответа на запрос о существовании перехода по текущему символу за необходимо хранить линейное количество информации от размера алфавита в каждой вершине. Поэтому, если алфавит очень большой требуется чрезмерный объём памяти. Можно сэкономить на памяти, храня в каждой вершине только те символы, по которым из неё есть переходы, но тогда поиск перехода будет занимать времени.
- Константное время на одну итерацию — это амортизированная оценка, в худшем случае одна фаза может выполняться за времени. Например, алгоритм Дэни Бреслауера и Джузеппе Итальяно, хоть и строит дерево за , но на одну итерацию в худшем случае тратит времени.
- На сегодняшний день существуют кэш-эффективные алгоритмы, превосходящие алгоритм Укконена на современных процессорах.
- Также алгоритм предполагает, что дерево полностью должно быть загружено в оперативную память. Если же требуется работать с большими размерами данных, то становится не так тривиально модифицировать алгоритм, чтобы он не хранил всё дерево в ней.
Время работы[править]
Для начала рассчитаем место, необходимое для выполнения алгоритма. Алгоритм использует рекурсивную функцию . Последовательность вызовов функции может занять память. Эта последовательность может быть представлена как путь корня рекурсивного дерева, до узла. Соответствующий вызов этого узла занимает памяти, каждый его «предок» занимает памяти, а остальные структуры используют . Очевидно, что любой путь от корня рекурсивного дерева до какого-то узла .
В итоге для работы алгоритма требуется памяти.
| Лемма (#2): |
| . |
| Доказательство: |
| Утверждение напрямую вытекает из и очевидного факта, что для любого множества , количество концов отрезков, лежащих в полосе , меньше чем . |
| Теорема (#1): |
| Доказательство: |
| Утверждение напрямую вытекает из и следующего отношения . |
Обозначим множество всех вершин рекурсивного дерева за .
| Теорема (#2): |
| Доказательство: |
| Для всех узлов, кроме корня имеет место выражение , следовательно . |
Начальная сортировка и инициализация множеств и может быть произведена за времени. Время работы функции является суммой длительностей всех его вызовов. Каждый вызов от внешних узлов добавляет к этой сумме . Для внутренних же узлов, время требуемое для поиска равно , а для остальных . Если мы все это сложим, то придем к выводу, что наш алгоритм работает за . Заметим, что его скорость можно увеличить до , если не будем учитывать время нахождения .
Соответственно в оптимальном алгоритме Балабана находится за .
Что дает обучение в школе “Алгоритм”
Обучение в нашей школе – это свобода воли каждого ученика. Есть возможность онлайн планировать расписание, контролировать домашнее задание и следить за отметками. Все это сопровождается комментариями учителей, что также можно посмотреть онлайн.

Более 100 педагогов-кураторов по отдельным предметам сопровождают учащихся на каждом этапе обучения. Все материалы, необходимые для обучения и самоподготовки, расположены на интерактивном учебном портале школы. Ребятам доступны ресурсы и все условия для дополнительного саморазвития, активного отдыха и занимательного досуга.
Мы гарантируем высокий уровень знаний, активное развитие и широкие возможности для поступления в любой российский и зарубежный ВУЗ, благодаря высоким экзаменационным результатам.
7. Стипендии
За хорошую учёбу и внеурочные активности школьники могут получить стипендию попечительского совета. Почти как в вузе, только претендентов на выплаты дети определяют сами. От каждого класса можно выдвинуть двух кандидатов по трём номинациям – талант, спорт и учёба – всего 50 учеников (с 4-го по 10-й классы).
После того, как кандидатов утвердит класс, их должен одобрить большой детский Совет, в который учителя не входят. И только потом претендентов оценит педсовет. Стипендиаты каждый месяц в течение полугода получают на карточку по 3 тыс. рублей. А выплаты по 20 тыс. рублей предусмотрены и для пяти лучших педагогов.



Улучшения алгоритма Шуфа
В 1990-х годах Ноам Элкис , а затем AOL Atkin , разработали улучшения базового алгоритма Шуфа, ограничив набор простых чисел, рассмотренных ранее, простыми числами определенного типа. Они стали называться простыми числами Элкиса и Аткина соответственно. Простое число называется простым числом Элкиса, если характеристическое уравнение: распадается , а простое число Аткина — это простое число, которое не является простым числом Элкиса. Аткин показал, как объединить информацию, полученную из простых чисел Аткина, с информацией, полученной из простых чисел Элкиса, для создания эффективного алгоритма, который стал известен как алгоритм Шуфа – Элкиса – Аткина . Первая проблема, которую необходимо решить, — определить, является ли данное простое число Элкисом или Аткином. Для этого мы используем модульные многочлены, которые появились в результате изучения модулярных форм и интерпретации как решеток. Как только мы определили, в каком случае мы находимся, вместо использования полиномов деления мы можем работать с полиномом, который имеет более низкую степень, чем соответствующий полином деления: а не . Для эффективной реализации используются вероятностные алгоритмы поиска корней, что делает его алгоритмом Лас-Вегаса, а не детерминированным алгоритмом. При эвристическом предположении, что примерно половина простых чисел до границы являются простыми числами Элкиса, это дает алгоритм, более эффективный, чем алгоритм Шуфа, с ожидаемым временем работы с использованием наивной арифметики и с использованием быстрой арифметики. Хотя известно, что это эвристическое предположение справедливо для большинства эллиптических кривых, известно, что оно верно не во всех случаях, даже при использовании GRH .
Sзнак равно{л1,…,лs}{\ Displaystyle S = \ {l_ {1}, \ ldots, l_ {s} \}}л{\ displaystyle l}ϕ2-тϕ+qзнак равно{\ Displaystyle \ phi ^ {2} -t \ phi + q = 0}Fл{\ displaystyle \ mathbb {F} _ {l}}О(л){\ Displaystyle О (л)}О(л2){\ Displaystyle О (л ^ {2})}О(журналq){\ Displaystyle О (\ журнал q)}О(журнал6q){\ Displaystyle О (\ журнал ^ {6} q)}О~(журнал4q){\ Displaystyle {\ тильда {O}} (\ log ^ {4} q)}
Сибирская региональная школа (колледж) Анны Муратовой

Сайт: http://anna-muratova-school.ruТелефон: +7 (983) 524-49-24, +7 (923) 037-94-76Стоимость: от 6500 р. в месяц в начальной школе
ЧПОУ «СРШ (колледж) Анны Муратовой» предлагает обучение и промежуточную аттестацию учеников с использованием электронного образовательного ресурса . Обеспечивается индивидуальный подход к каждому обучающемуся, формируем личную траекторию учебных достижений в образовании.
Преимущество дистанционных занятий – выбор удобного для ребенка времени и отсутствие пространственного и временного ограничения в учебе. Занятия в Школе полезно совмещать как с очным, так и с домашним обучением. Они заменят репетитора при повторении материала и помогут усвоить новые темы, если учеба дается нелегко и требует дополнительного объяснения.
В школу можно зачисляться для прохождения промежуточной аттестации не только по предметам комплексного школьного курса за определённый класс, то есть по всем предметам образовательной программы определенного класса, но и аттестоваться по отдельным предметам совершенно независимо от наличия аттестации по каким–либо другим предметам.
Школа предлагает к освоению и программы дополнительного образования, а также программы изучения или совершенствования иностранного языка (английский, немецкий, французский, испанский, итальянский, португальский, китайский).
4. Шведский стол
Столовая в «Алгоритме успеха» работает по системе шведский стол. Это значит, что ученики могут сами выбрать, что они хотят съесть сегодня: в мясной день, к примеру, им предложат сразу три блюда из мяса, приготовленные разными методами (варёное, тушёное, котлета). Три разных блюда – в рыбный день. И так каждый день.
В школе постоянно экспериментируют с меню и корректируют его с нового учебного года. Повара гордятся тем, что научили ребят есть молочные каши на завтрак и даже брокколи, к которым поначалу дети были абсолютно равнодушны.
Столовая вмещает 380 детей, поэтому едят они по расписанию: пока обедают 2–5-е классы, остальные гуляют на улице. И наоборот. 40-минутная прогулка каждый день – обязательная часть школьного дня.



Центр Семейного Образования «Репетитор плюс школа»
Возраст: от 7 летСайт: http://schoolrepetitor.ru/Телефон: 8 (977) 841- 98-48Стоимость: от 5000 рублей
Центр Семейного Образования «Репетитор плюс школа» предлагает разные формы обучения:
- Онлайн-обучение;
- Репетиторы по всем школьным предметам (онлайн);
- Аттестация (Прикрепление/Сопровождение);
- Семейное обучение
- Помощь в выполнении домашних заданий;
- Экстернат для школьников и лиц старше 18 лет.
Хотите ли Вы подтянуть отдельные предметы, подготовиться к ОГЭ/ЕГЭ или полностью перевести ребёнка на обучение по индивидуальной программе — в Центре Семейного Образования «Репетитор плюс школа» созданы прекрасные условия для этого.
Занятия проводят лучшие преподаватели, выпускники ведущих ВУЗов страны (МГУ имени М.В. Ломоносова, МГТУ им. Н.Э. Баумана, РШЭ, МГПУ и т.д.), знающие программы и требования при проведении ОГЭ, ЕГЭ и олимпиад, и имеющие большой стаж работы со школьниками разных возрастов.
Вся команда Центра Семейного Образования «Репетитор плюс школа» знает, как найти подход к каждому ребенку, как сделать процесс обучения интересным и полезным, как поддержать и помочь каждому ученику на всем пути обучения.
Работа Центра выстроена по определенному алгоритму: диагностика уровня знаний ученика, подбор преподавателя с учетом индивидуальных предпочтений, освоение материала и детальная его проработка.
Решили, что ребенку нужен репетитор, но не знаете, какому специалисту отдать предпочтение? Тьюторы Центра расскажут вам, как выбрать репетитора и обезопасить ребенка от многолетних, но безрезультатных занятий.
В случае необходимости, поможем подготовиться к Промежуточной/Итоговой аттестации не выходя из дома ·
- Полная поддержка.
- Персональный куратор.
- Онлайн-занятия по всем предметам школьной программы.
- Индивидуальные занятия с репетиторами.
В Центре используют все формы эффективной подготовки школьников, авторские методики преподавания и педагоги высокого уровня.
Разбираем «на пальцах»
Вот Алексей. Он обычный парень, который любит играть в футбол. Нам необходимо прописать программу, симулирующую игру Лёши. Для этого мы прописываем конкретную инструкцию, которая состоит из таких команд:
-
Надеть спортивную одежду.
-
Взять мяч.
-
Выйти на улицу.
-
Поставить мяч на землю.
-
Ударить по мячу.

Запускаем игру и понимаем, что что-то идёт не так. Причина в том, что Алексей вышел играть в туфлях, а не в спортивной обуви, так как мы не учли в инструкции этот нюанс.
Возвращаемся назад и дополняем:
-
Надеть спортивную одежду.
-
Надеть спортивную обувь.
-
Взять мяч.
-
Выйти на улицу.
-
Поставить мяч на землю.
-
Ударить по мячу.
Теперь игра идёт так, как мы задумали.
Этот вариант примитивный. В настоящей программе инструкций будет гораздо больше. Каждое действие Алексея придётся прописывать подробно. Например, выход из дома:
-
Открыть дверь.
-
Выйти.
-
Закрыть дверь.
-
Подойти к лифту.
-
Нажать на кнопку.
-
Зайти в лифт.
-
Нажать кнопку первого этажа.
-
Выйти из лифта и т. д.
Чем подробнее прописаны стейтменты, тем более качественно работает программа.
Представьте количество команд, инструкций и сложность алгоритма в искусственном интеллекте или роботе. Сколько подробных инструкций предусматривает и прописывает программист, чтобы искусственный интеллект самостоятельно принимал решения, а робот ходил, разговаривал, отвечал и реагировал на действия.
В случае с Алексеем, дополнительно понадобилось бы прописать и то, что он идёт на выбранную спортивную площадку или стадион, зовёт с собой друзей и т. д.
Учитывайте тот факт, что ваша программа обязательно будет изменяться и дополняться. Тот, кто после вас займётся её поддержкой и развитием, должен понять вашу логику. Не слишком стремитесь к упрощению и минималистичности.
Электронная гимназия АНПОО «МАНО»

Сайт: http://eschool.mano.pro/Телефон: 8 800 100 84 42, 8 (3812) 95-10-37Стоимость: от 500 рублей
Электронная гимназия АНПОО «МАНО» обучает школьников с 1 по 11 класс.
Создана с применением дистанционных образовательных технологий, порядок применения которых регламентирован Министерством просвещения РФ.
В гимназии представлены все предметы школьной программы, которые разработаны в соответствии с ФГОС. Учебные материалы (видеоуроки, конспекты, тесты, тренажёры) доступны в любое время. К каждому ученику гимназии обеспечивается индивидуальный подход.
Преимущества гимназии:
- удобная организация процесса обучения,
- отсутствие пространственного и временного ограничения в учебе,
- доступность материала в любое время с любых электронных носителей,
- возможность повторения урока неограниченное количество раз,
- видео с объяснением учителя для каждого урока,
- интерактивные тесты к каждому уроку,
- возможность обучения в каникулы и во время карантина.
Обучаясь в гимназии, Вы сможете:
- получить аттестат государственного образца;
- подготовится к сдаче ВПР, ОГЭ, ЕГЭ;
- подтянуть отдельные предметы, которые Вам необходимы.
Гимназия может заменить репетитора при повторении материала и поможет усвоить новые темы, если учеба дается нелегко или требует дополнительного объяснения.
В гимназию можно зачисляться для прохождения промежуточной аттестации как по всем предметам образовательной программы определенного класса, так и по отдельным предметам.
Вы можете самостоятельно выбрать удобное время и определить темп просмотра заданий, время выполнения которых не ограничено.
В создании уроков принимали участие лучшие преподаватели: кандидаты и доктора педагогических наук, высококвалифицированные специалисты, имеющие большой опыт профессиональной работы в области педагогики, психологии, менеджмента, инновационной деятельности.
В процессе обучения в гимназии учителя проверят выполненные задания, выставят оценку в электронный журнал и помогут разобрать ошибки.
Также электронная гимназия предлагает Вам авторские онлайн-курсы для детей младших и старших классов:
- Школа шахмат «Mano Chess» (поступенчатый курс с нуля до уверенного шахматиста, с 6 лет);
- Школа бизнеса и трейдинга «Bussines Land» (курс обучит основам ведения бизнеса-трейдинга, разработан для учеников начиная с 5 класса);
- Школа «Компьютерного моделирования и программирования на языке C#» (курс обучит основам моделирования и программирования на языке C#», разработан для учеников начиная с 7 класса).
По окончание курсов вы получите официальные документы о дополнительном образовании.
Теорема Хассе
Теорема Хассе утверждает, что если — эллиптическая кривая над конечным полем , то удовлетворяет
EFq{\ Displaystyle E / \ mathbb {F} _ {q}}Fq{\ displaystyle \ mathbb {F} _ {q}}#E(Fq){\ Displaystyle \ #E (\ mathbb {F} _ {q})}
- ∣q+1-#E(Fq)∣≤2q.{\ displaystyle \ mid q + 1 — \ # E (\ mathbb {F} _ {q}) \ mid \ leq 2 {\ sqrt {q}}.}
Этот мощный результат, представленный Хассе в 1934 году, упрощает нашу проблему, сужая до конечного (хотя и большого) набора возможностей. Определяя быть и используя этот результат, мы теперь имеем, что вычисление значения по модулю где , достаточно для определения , и, следовательно . Несмотря на то , что не существует эффективный способ вычислить непосредственно для общих , можно вычислить для достаточно эффективно небольшого штриха,. Мы выбираем набор различных простых чисел, таких что . Учитывая все , китайская теорема об остатках позволяет нам вычислить .
#E(Fq){\ Displaystyle \ #E (\ mathbb {F} _ {q})}т{\ displaystyle t}q+1-#E(Fq){\ displaystyle q + 1 — \ # E (\ mathbb {F} _ {q})}т{\ displaystyle t}N{\ displaystyle N}N>4q{\ displaystyle N> 4 {\ sqrt {q}}}т{\ displaystyle t}#E(Fq){\ Displaystyle \ #E (\ mathbb {F} _ {q})}т(модN){\ Displaystyle т {\ pmod {N}}}N{\ displaystyle N}т(модл){\ Displaystyle т {\ pmod {l}}}л{\ displaystyle l}Sзнак равно{л1,л2,…,лр}{\ Displaystyle S = \ {l_ {1}, l_ {2}, …, l_ {r} \}}∏лязнак равноN>4q{\ displaystyle \ prod l_ {i} = N> 4 {\ sqrt {q}}}т(модля){\ Displaystyle т {\ pmod {l_ {я}}}}ля∈S{\ displaystyle l_ {i} \ in S}т(модN){\ Displaystyle т {\ pmod {N}}}
Чтобы вычислить простое число , мы воспользуемся теорией эндоморфизма Фробениуса и полиномов с делением
Обратите внимание, что рассмотрение простых чисел — это не потеря, так как мы всегда можем выбрать большее простое число на его место, чтобы гарантировать, что продукт достаточно большой. В любом случае для решения этого случая чаще всего используется алгоритм Шуфа, поскольку существуют более эффективные, так называемые адические алгоритмы для полей с малой характеристикой.
т(модл){\ Displaystyle т {\ pmod {l}}}л≠п{\ displaystyle l \ neq p}ϕ{\ displaystyle \ phi}л≠п{\ displaystyle l \ neq p}qзнак равноп{\ displaystyle q = p}п{\ displaystyle p}
Выводы
Соберём всё, что мы отметили рассматривая разные примеры «действия»:
- «действие» можно использовать для создания алгоритма;
- «действие» может быть элементарным;
- «действие» может быть реализовано алгоритмом;
- в «действии» обязательно участвует некоторый объект или группа объектов;
- для группы объектов «действие» происходит только тогда, когда эти объекты «достаточно близко»;
- в действии изменяются связи и параметры объектов (включая параметры их движения);
- «действие» всегда и обязательно должно быть повторимо.
Признак Повторимости помогает нам в создании наших алгоритмов. С его использованием мы из всех процессов выделяем те, что являются «действием» и на их основе создаём новые алгоритмы. Более того этот признак достаточно прост и на основе его формализации можно снизить требования к системе обнаруживающей и создающей «действия» и поручить это нашему компьютеру.
Следующая статья серии (Часть 2) будет посвящена рассмотрению способов, с использованием которых «действия» могут быть сгруппированы в алгоритм. Этих способов достаточно много и есть предпосылки, что их описание не получится уместить в одну статью. Напишем — увидим.
Спасибо Вам за внимание



